1. Задание № 258 

Сложность: II
Классификатор алгебры: 3\.8\. Неравенства высших степеней
Линейные, квадратные, степенные неравенства
i
Сумма всех натуральных решений неравенства 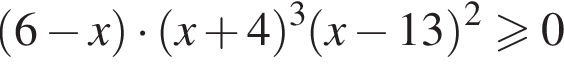 равна:
равна:
1) 11
2) 19
3) 21
4) 34
5) 36
Решение. Неравенство выполнеятся при  и при
и при 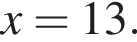 Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.
Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.
Правильный ответ указан под номером 4.
Ответ: 4
258
4
Сложность: II
Классификатор алгебры: 3\.8\. Неравенства высших степеней
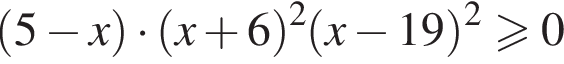 равна:
равна: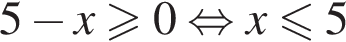 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 19. Их сумма равна 34.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 19. Их сумма равна 34. равна:
равна: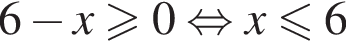 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 17. Их сумма равна 38.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 17. Их сумма равна 38.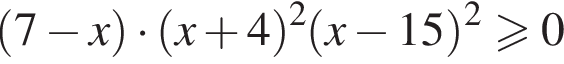 равна:
равна: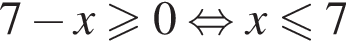 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 15. Их сумма равна 43.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 15. Их сумма равна 43.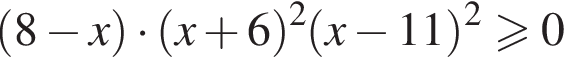 равна:
равна: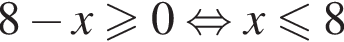 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 8, 11. Их сумма равна 47.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 8, 11. Их сумма равна 47.